Given the graph below, is it possible to construct a path (or a cycle, i.e. a path starting and ending on the same vertex) which visits each edge exactly once ?
All vertices in a graph for which an Euler circuit exists must have even degree.
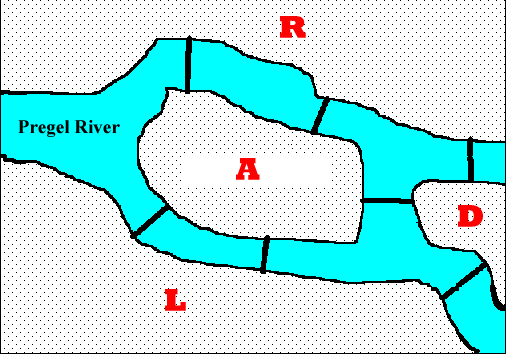
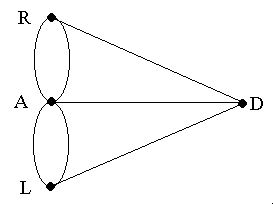
The first thing that Euler did was boil the Konigsberg problem down to its
essentials by stripping away all irrelevant material:
- the shapes and sizes of the land masses don't matter - turn them
into points
- all that matters about the bridges is how they connect the land
masses - make them into lines connecting the points
- having done that, it is not necessary to actually depict the river
to study the problem - leave it out
What results is an abstract representation of Konigsburg that depicts just
enough (and not a whit more) about the problem to completely describe it. This
simplified form of the problem makes it easier to study as a mathematical
object, and to devise some mathematical theorems about it. Which is exactly
what Euler did.
The sum of the degrees of all vertices in any graph is twice the number of edges.
